Semi-Magic Square Knight's Tours
For years, even for centuries, chess and Knight's Tour enthusiasts have wondered how many different Knight's Tours exist whether they be open or closed tours. Also, they wanted to know if any Knight's Tours could make complete magic squares where all the rows, columns, and main diagonals would add up to the same number (260) after putting a number for each Knight's move on all 64 squares it visited.
Here are some numbers found on the Internet that I have not personally verified.
33,439,123,484,294 unoriented Knight's Tours
26,534,728,821,064 closed directed Knight's Tours
13,267,364,410,532 undirected Knight's Tours
1,692,674,826,245 Closed Knight's Tours (but less if removing tours with reflection/rotation symmetries)
One thing I do know for sure is that there are NO magic square Knight's Tours where both main diagonals add to 260 on an 8x8 square chessboard, but there are exactly 140 unique or independent semi-magic square Knight's Tours. Unique or independent means that tours with equal symmetries such as reflections or rotations of the same tour are not counted, elsewise there would be a total of 158 semi-magic square Knight's Tours.
I worked with a team from around the world that spent countless CPU hours, well actually the program counted them, crunching an algorithm's code that searched for magic Knight's Tours but finding only 140 unique Semi-Magic Knight's Tours.
Ok, if you really must know how long it took to find all 140 Semi-Magic Knight's Tours, here is the original data from August 05, 2003, when the program completed the search on many different CPUs around the world, including mine. Wow, 20 years ago! Seems like yesterday.
I copied the above listed results from Magictour.free.fr belonging to Guenter Stertenbrink. Check out the site to see messages included about Magic/Semi-Magic Knight's Tours, code samples, and other good info from 2003 to the present.
In 2019, Yann Denef's updated program and faster computer (AMD Ryzen 5 1600X - 3.6GHz) completed the search for Semi-Magic Knight's Tours in about 22 hours, much better than 61.4 days back in 2003.
Without the aid of a computer, I've easily created many more Knight's Tours and even a Semi-Magic Square Knight's Tour where all the rows and columns add up to the same number. In fact, every other vertical pair of numbers adds up to 49 and 81 respectively while the four major quadrants each add up to 520 and the four main sets of 2x2 squares in each quadrant add up to 130. The numbers 49 and 81 are significant since 49 is 7 squared in which 7 represents the shape of the Knight's move. Also, 81 is 9 squared in which 9 represents the first known Magic Square (3x3 square or 9 squares) from about 2200 B.C.
Here are some numbers found on the Internet that I have not personally verified.
33,439,123,484,294 unoriented Knight's Tours
26,534,728,821,064 closed directed Knight's Tours
13,267,364,410,532 undirected Knight's Tours
1,692,674,826,245 Closed Knight's Tours (but less if removing tours with reflection/rotation symmetries)
One thing I do know for sure is that there are NO magic square Knight's Tours where both main diagonals add to 260 on an 8x8 square chessboard, but there are exactly 140 unique or independent semi-magic square Knight's Tours. Unique or independent means that tours with equal symmetries such as reflections or rotations of the same tour are not counted, elsewise there would be a total of 158 semi-magic square Knight's Tours.
I worked with a team from around the world that spent countless CPU hours, well actually the program counted them, crunching an algorithm's code that searched for magic Knight's Tours but finding only 140 unique Semi-Magic Knight's Tours.
Ok, if you really must know how long it took to find all 140 Semi-Magic Knight's Tours, here is the original data from August 05, 2003, when the program completed the search on many different CPUs around the world, including mine. Wow, 20 years ago! Seems like yesterday.
- As of August,05.,2003 136 ranges have been checked.
- 5305279.08 seconds = 61.40 days of computation time were needed
- CPUs went through 11_945038 Gigacycles = 138.25 days with 1GHz
- 52_280100_180652 knight moves were done, that's 228.5 CPU-cycles per move (=node)
- between 7.0e10 and 3.1e12 nodes per range, average 3.8e11, deviation 5.4e11
I copied the above listed results from Magictour.free.fr belonging to Guenter Stertenbrink. Check out the site to see messages included about Magic/Semi-Magic Knight's Tours, code samples, and other good info from 2003 to the present.
In 2019, Yann Denef's updated program and faster computer (AMD Ryzen 5 1600X - 3.6GHz) completed the search for Semi-Magic Knight's Tours in about 22 hours, much better than 61.4 days back in 2003.
Without the aid of a computer, I've easily created many more Knight's Tours and even a Semi-Magic Square Knight's Tour where all the rows and columns add up to the same number. In fact, every other vertical pair of numbers adds up to 49 and 81 respectively while the four major quadrants each add up to 520 and the four main sets of 2x2 squares in each quadrant add up to 130. The numbers 49 and 81 are significant since 49 is 7 squared in which 7 represents the shape of the Knight's move. Also, 81 is 9 squared in which 9 represents the first known Magic Square (3x3 square or 9 squares) from about 2200 B.C.
Semi-Magic Square Knight's Tour
With a little bit of research, you will find that others such as William Beverley have created similar Semi-Magic Square Knight's Tours. Unlike William Beverley, I've taken an additional step by creating a simple game that will allow anyone to easily make beautiful mathematical Knight's Tour art.
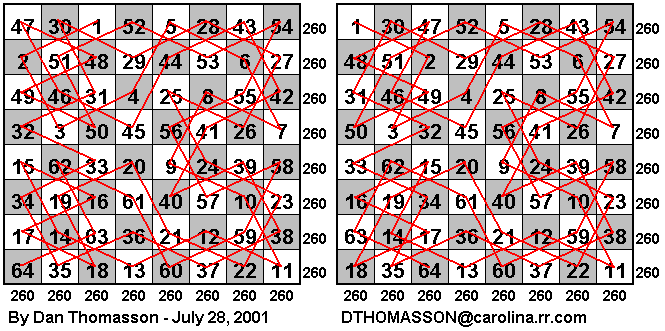
Here are a couple Semi-Magic Knight's Tours that are almost identical. Notice how the first and third columns from the left are interchangeable. I thought I was quite clever coming up with these patterns until I found out that William Beverley designed the first such tour with the same path pattern of the Knight around 1847-1848.
Here are a couple Semi-Magic Knight's Tours that are almost identical. Notice how the first and third columns from the left are interchangeable. I thought I was quite clever coming up with these patterns until I found out that William Beverley designed the first such tour with the same path pattern of the Knight around 1847-1848.
Semi-Magic Knight's Tours alternating vertical number pairs adding to 49 and 81 respectively.
Semi-Magic Knight's Tour by William Beverley (1812-1889)