Knight's Tour Latin Squares I
I bet you are wondering what the heck does Knight's Tours have to do with Latin Squares. Well, you might just be surprised to find out that Knight's Tours can make amazing Latin Squares. Before I forget, I guess I should define what a Latin Square is for those that do not know. As seen in one of my other Knight's Tour webpages, a dictionary definition might be confusing.
"noun
plural noun: Latin squares
For the purpose of this webpage, let's use the following Wikipedia definition that applies more accurately.
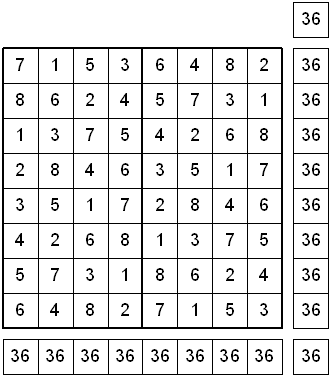
Therefore, for our purpose, a Latin Square contains a series of numbers from 1-8 or 2-9 that when placed in an 8x8 grid square, no numbers repeat themselves in the same row or the same column. Here is an example:
"noun
plural noun: Latin squares
- an arrangement of letters or symbols that each occur n times, in a square array of n 2 compartments so that no letter appears twice in the same row or column.
- a Latin square used as the basis of experimental procedures in which it is desired to control or allow for two sources of variability while investigating a third."
For the purpose of this webpage, let's use the following Wikipedia definition that applies more accurately.
- "In combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column."
Therefore, for our purpose, a Latin Square contains a series of numbers from 1-8 or 2-9 that when placed in an 8x8 grid square, no numbers repeat themselves in the same row or the same column. Here is an example:
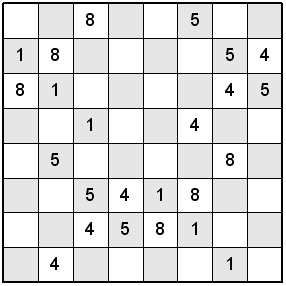
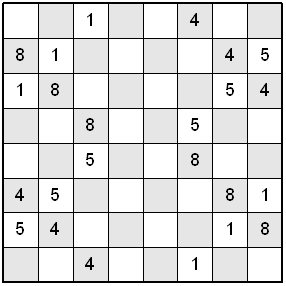
Take a look at the following Knight's Tour Latin Square puzzles.
Try solving the Knight's Tour Latin Square puzzles shown above. Hint, after solving the squares, you should be able to draw four separate 16-Move Closed Knight's Tours in each square. If you are unable to solve the problems, click on the Knight's Tour Latin Squares above to see their S-O-L-U-T-I-O-N.
On 2-23-2025, Ben Schultz emailed me the following:
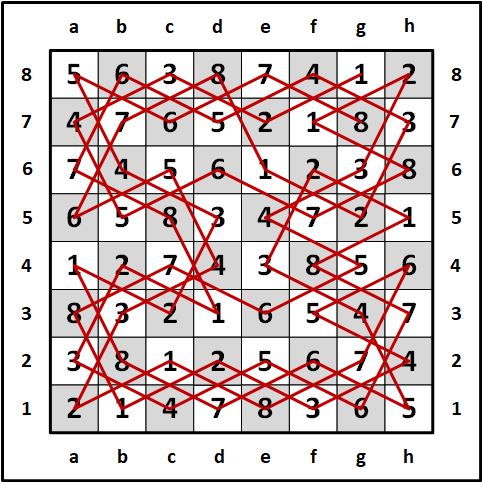
"hi! hope you're well, sir! Here's a Latin square using a single knight's tour to cover the whole board. I saw your work from 20 years ago after independently trying this. I think we are trying the same thing. In any case, just to reiterate, the idea is to go from 1-8 (each number in the Latin square) sequentially. I've used colours (British spelling) here for aesthetic reasons." The following image is a collaboration between Ben and his friend who is nick-named Paws. Paws found this Latin square and Ben redrew it.
"hi! hope you're well, sir! Here's a Latin square using a single knight's tour to cover the whole board. I saw your work from 20 years ago after independently trying this. I think we are trying the same thing. In any case, just to reiterate, the idea is to go from 1-8 (each number in the Latin square) sequentially. I've used colours (British spelling) here for aesthetic reasons." The following image is a collaboration between Ben and his friend who is nick-named Paws. Paws found this Latin square and Ben redrew it.
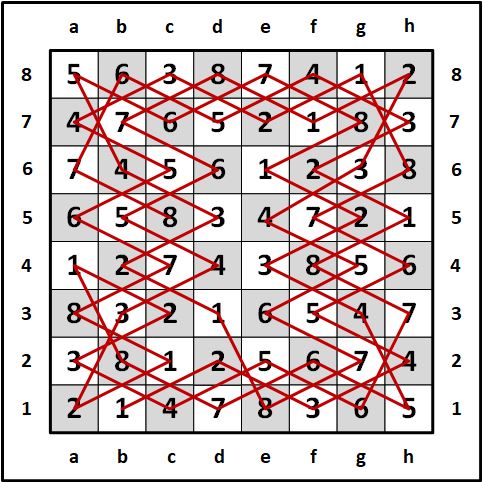
Using algebraic chess notation, follow the knight's moves: (1) g8 (brown), (2) e7 (purple), (3) c8 (pink), (4) a7 (blue), (5) b5 (green), (6) d6 (yellow), (7) f5 (orange), (8) h6 (red). Start the count move over with (1) c7 (brown), etc. around the board. Adding the numbers 1 - 8 respectively to their colored squares will result in a complete 8 x 8 Latin square using a single open knight's tour that covers all squares of the 8 x 8 board.
The following knight's tour Latin square also came from Ben Schultz on 2-23-2025:
The following knight's tour Latin square also came from Ben Schultz on 2-23-2025:
There is a unique matching pattern between both knight tours that Ben provided. The patterns are similar to my knight's tour Latin square puzzles shown above on this page. Though the knight tours that he shared look different, the internal pattern (the key) in both tours is the same with different move orders.
First, divide the boards into half both vertically and horizontally. Taking the right vertical half and rotate it 180 degrees will show that all its numbers exactly match the numbers of the left vertical half of squares. The same process can be done to the bottom horizontal half where the numbers will match the top horizontal half of numbers after rotating either half by 180 degrees.
Using chess algebraic notation, (reverse Ben's numbers so that 1 represents the bottom row and 8 for the top row) check out the following keys that make a mirrored pattern vertically and horizontally between both halves. In the first knight's tour Latin square by Ben and his friends shown above, check out the crossing patterns of 6 (b8) - 6 (c7) - 6 (d6) with 5 (b5) - 5 (c6) - 5 (d7) and 1 (e6) - 1 (f7) - 1 (g8) with 2 (e7) - 2 (f6) -2 (g5) in the top half and 2 (b4) - 2 (c3) - 2 (d2) with 1 (b1) - 1 (c2) - 1 (d3) and 5 (e2) - 5 (f3) - 5 (g4) with 6 (e3) - 6 (f2) - 6 (g1) in the bottom half. See illustrations below showing this pattern for each knight's tour Latin square.
First, divide the boards into half both vertically and horizontally. Taking the right vertical half and rotate it 180 degrees will show that all its numbers exactly match the numbers of the left vertical half of squares. The same process can be done to the bottom horizontal half where the numbers will match the top horizontal half of numbers after rotating either half by 180 degrees.
Using chess algebraic notation, (reverse Ben's numbers so that 1 represents the bottom row and 8 for the top row) check out the following keys that make a mirrored pattern vertically and horizontally between both halves. In the first knight's tour Latin square by Ben and his friends shown above, check out the crossing patterns of 6 (b8) - 6 (c7) - 6 (d6) with 5 (b5) - 5 (c6) - 5 (d7) and 1 (e6) - 1 (f7) - 1 (g8) with 2 (e7) - 2 (f6) -2 (g5) in the top half and 2 (b4) - 2 (c3) - 2 (d2) with 1 (b1) - 1 (c2) - 1 (d3) and 5 (e2) - 5 (f3) - 5 (g4) with 6 (e3) - 6 (f2) - 6 (g1) in the bottom half. See illustrations below showing this pattern for each knight's tour Latin square.
Knight's Tour Latin Square 1
Knight's Tour Latin Square 2
Knight's Tour Latin Square 3
The pattern in knight's tour Latin square 3 is the reverse pattern from the Latin square 2 shown above. Notice how similar the Latin square 3 is to Latin square 1. By systematically and equally increasing or decreasing all the numbers in the above knight's tour Latin squares, many additional knight's tours can be found that make Latin squares. I will let the reader solve these puzzles. Enjoy!!! Oh yeah, thanks for Ben and his friends for providing these ideas and excellent knight's tour Latin squares.
I also realized that both tours from Ben and Paws make the same Latin square. The second tour that I made is the same as Ben's tour but rotated 180 degrees. Increasing or decreasing all the numbers equally in the Latin square will still accommodate both knight's tours.
I used the following key to make the two knight's tour Latin squares shown above. This key is really the same key as Knight's Tour Latin Square 1 but adding the corner numbers.
I made another knight's tour from the same Latin square numbers shown above. This tour is very similar to the knight's tour by Paws. However, my tour can also make a neat tessellation.
The following four partial open tours come from the blue, red, green, and orange paths of the knight shown above.
Closing the partial tour patterns look like the following pieces that can be combined as a single tessellation piece.
Here is what the tessellation piece looks like.
Finally, the knight's tour pieces can make the following tessellation that can be expanded upon to make book covers, webpage backgrounds, tiles, or other types of art. Simply change the colors to your liking when designing other tessellations using these patterns. Don't forget to look at my KT Tessellation page under the KT Art heading and other KT Latin Squares under the KT Latin Squares 1 heading.
Remember to reference my name and website if you copy anything from it or want to reuse/repost it on other websites or books. I prefer to be contacted to get my permission prior to using my work (email - danthomasson52@gmail.com). If you have other neat knight's tour art, or ideas, please let me know. I will be glad to share your work on this website.