Knight's Tour Latin Squares II
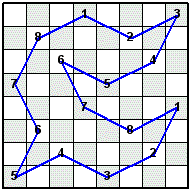
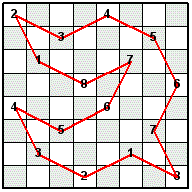
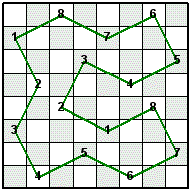
Check out the Knight's Tour Tessellation Construction II page that shows how to make a single open knight's tour circuit out of the same four mini-knight's tours shown above.
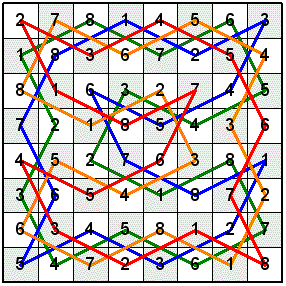
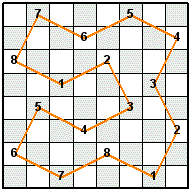
In the Knight's Tour Latin Square shown above, only one instance of each integer from 1 to 8 is in each row and column. The following four 16-Move Mini-Knight's Tours were combined to make the Latin Square. The Knight's moves for each tour are numbered from 1 to 8, then 1 to 8 is repeated a second time to complete the tour.
In the Knight's Tour Latin Square shown above, only one instance of each integer from 1 to 8 is in each row and column. The following four 16-Move Mini-Knight's Tours were combined to make the Latin Square. The Knight's moves for each tour are numbered from 1 to 8, then 1 to 8 is repeated a second time to complete the tour.
After filling in the four tours shown above with the same color as their line color, they can be combined into one piece that can be tessellated.
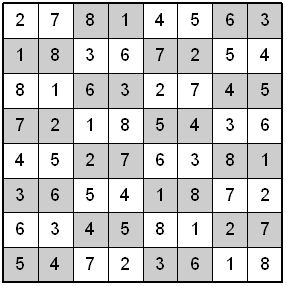
There are all sorts of fun math oddities that can be found within this Knight's Tour Latin Square. Notice in the diagram below on the left that each alternating horizontal number pair adds up to 9. Also, if you take the alternating horizontal number pairs as one number each (i.e. 2 and 7 as 27), they are multiples of 9 (i.e. 27 is 9x3).
Alternating groups of 4 numbers each are shown in the above Latin Square on the right. Consider each group of 4 numbers as one number (i.e. 2, 7, 8, 1 as 2781). Divide 2781 by 9 to get 309. Do the same thing to all the 4-digit numbers on the left half of the square. Add up these 8 numbers to get 4444. Now do the same thing to the right half of the square. Notice that they also add up to 4444.
2781 / 9 = 309 4563 / 9 = 507
1836 / 9 = 204 7254 / 9 = 806
8163 / 9 = 907 2745 / 9 = 305
7218 / 9 = 802 5436 / 9 = 604
4527 / 9 = 503 6381 / 9 = 709
3654 / 9 = 406 1872 / 9 = 208
6345 / 9 = 705 8127 / 9 = 903
5472 / 9 = 608 3618 / 9 = 402
4444 4444
1836 / 9 = 204 7254 / 9 = 806
8163 / 9 = 907 2745 / 9 = 305
7218 / 9 = 802 5436 / 9 = 604
4527 / 9 = 503 6381 / 9 = 709
3654 / 9 = 406 1872 / 9 = 208
6345 / 9 = 705 8127 / 9 = 903
5472 / 9 = 608 3618 / 9 = 402
4444 4444
When all the numbers are divided by 9, the results are 3-digit numbers with a zero in the middle. Also, the digits on either side of the zero for the first eight 3-digit results on the left side of the board, contain each of the digits from 2-9. The same occurs for the 3-digit results on the right side of the board.
I found it interesting that 4444 is also the exact number of solutions to the excellent "Calmplex puzzle" designed by Andrew Snowie in Canada.
Look at the results when doing the same dividing/adding process for each entire row:
I found it interesting that 4444 is also the exact number of solutions to the excellent "Calmplex puzzle" designed by Andrew Snowie in Canada.
Look at the results when doing the same dividing/adding process for each entire row:
27814563 / 9 = 3090507
18367254 / 9 = 2040806
81632745 / 9 = 9070305
72185436 / 9 = 8020604
45276381 / 9 = 5030709
36541872 / 9 = 4060208
63458127 / 9 = 7050903
54723618 / 9 = 6080402
44444444
18367254 / 9 = 2040806
81632745 / 9 = 9070305
72185436 / 9 = 8020604
45276381 / 9 = 5030709
36541872 / 9 = 4060208
63458127 / 9 = 7050903
54723618 / 9 = 6080402
44444444
Let's see how we can make a new 8x8 Magic Latin Square from the previous eight 8-digit results. All the rows, columns, and main diagonals should each add up to 44.
1. Remove all the zeros in each number to get the following eight 4-digit numbers.
3957
2486
9735
8264
5379
4628
7593
6842
2. Place these eight 4-digit numbers down the left side of an 8x8 grid square as shown in the square below.
1. Remove all the zeros in each number to get the following eight 4-digit numbers.
3957
2486
9735
8264
5379
4628
7593
6842
2. Place these eight 4-digit numbers down the left side of an 8x8 grid square as shown in the square below.
3. Reverse the order (vertically flip) of the eight 4-digit numbers and place them down the right side of the same square as shown above.
4. Add up all the rows, columns, and main diagonals to get 44 for each one.
5. Subtract "1" from all the digits inside the square to get a new Magic Constant of 36.
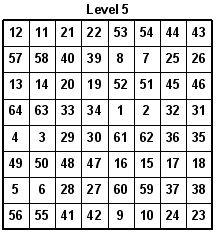
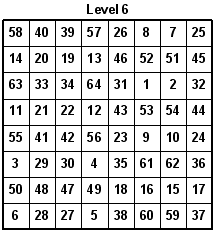
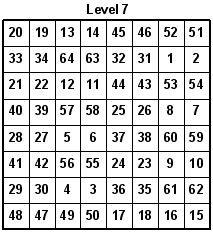
With the new 8x8 Magic Latin Square, we can make an 8x8x8 Magic Latin Cube where even the main diagonals of all faces of the cube, and the major internal diagonals equals 44. Also, all rows, columns, and pillars equal 44. Look at the eight levels. One row is rotated up each time to create a new level.
4. Add up all the rows, columns, and main diagonals to get 44 for each one.
5. Subtract "1" from all the digits inside the square to get a new Magic Constant of 36.
With the new 8x8 Magic Latin Square, we can make an 8x8x8 Magic Latin Cube where even the main diagonals of all faces of the cube, and the major internal diagonals equals 44. Also, all rows, columns, and pillars equal 44. Look at the eight levels. One row is rotated up each time to create a new level.
There are several number groups based on the number 9, or multiples of 9, that can be found in the original Knight's Tour Latin Square. Here are a couple groups. See what other groups you can find.
Here is another Latin Cube I designed that is based on a Magic Square originating from 3-d Knight Moves. All rows, columns, main diagonals, and pillars each add up to 260.
Here is another Latin Cube I designed that is based on a Magic Square originating from 3-d Knight Moves. All rows, columns, main diagonals, and pillars each add up to 260.
I'd like to thank Guenter Stertenbrink for indirectly giving me the idea to create Knight's Tour Latin Squares when he mentioned he was interested in working on Sudoku Knight's Tour problems. Latin Squares and Sudoku problems are very similar in their construction, but I find the constraints of the 3x3 squares in Sudoku problems to be a bit of an issue when creating Knight's Tours. I did, however, design an Order 36 Sudoku based on a 6x6 closed Knight's Tour.