Knight's Tour Semi-magic
​ Square Construction II

While making designs on the chessboard with four mini-knight's tour open circuits, I realized I could construct a complete semi-magic knight's tour covering all 64 squares with one circuit.  Check out the following steps I used in making the knight's tour.

Step 1:

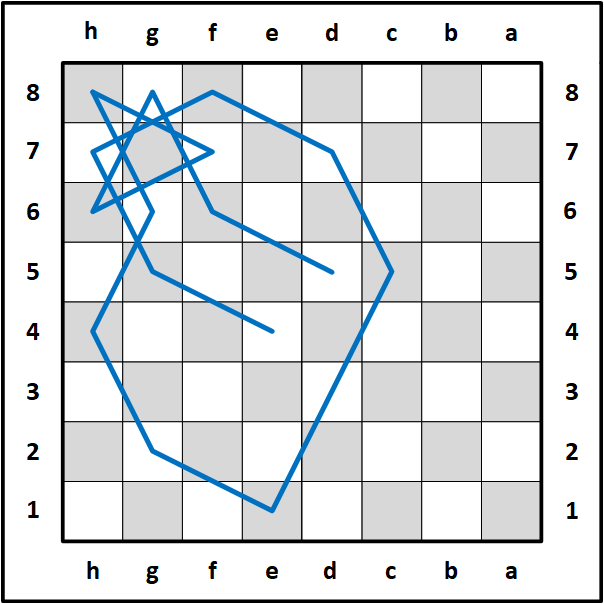
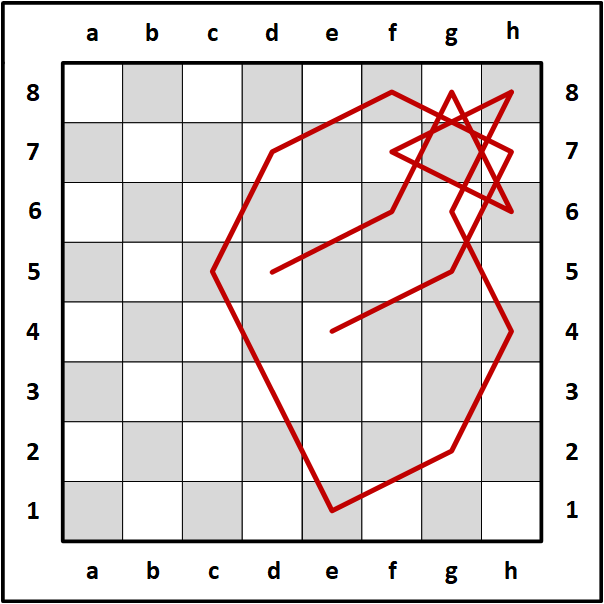
I first made one complete circuit consisting of 16 moves in blue then copied the circuit and flipped it horizontally to make the second circuit and colored the moves red.

Step 2:

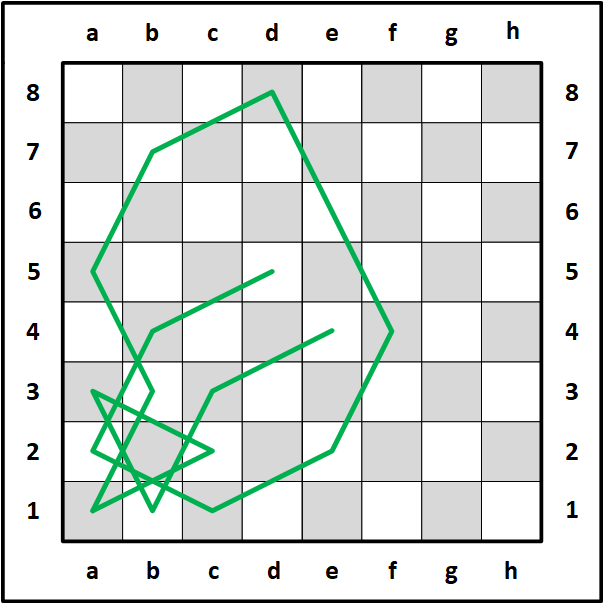
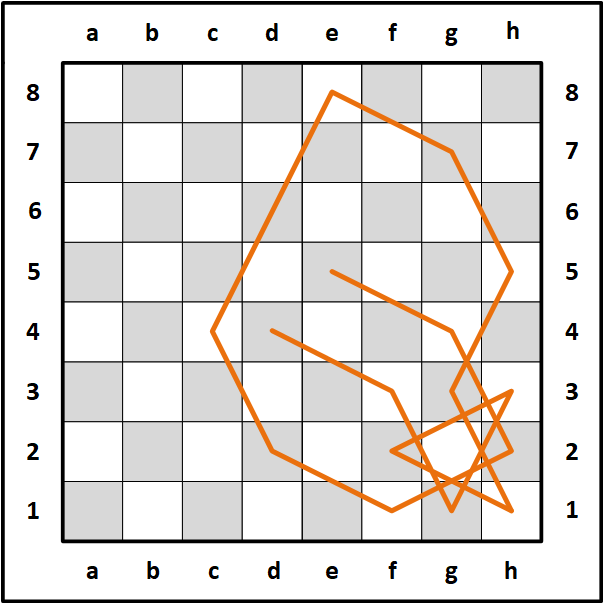
I then flipped the first two circuits vertically and colored the moves green and orange respectively.

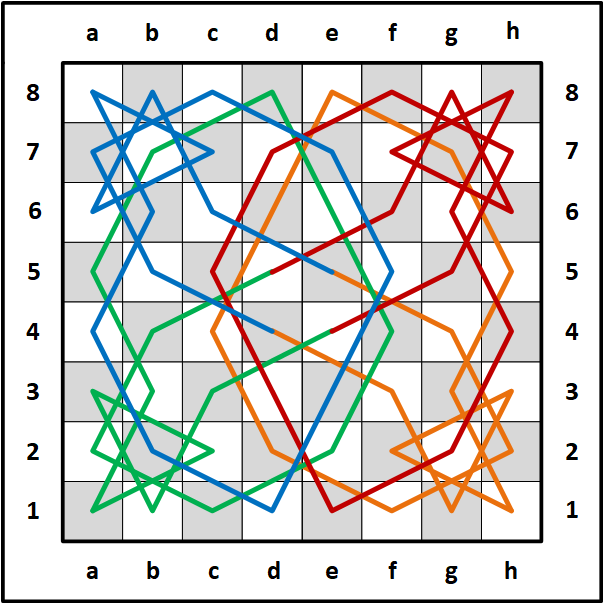
Here are the same four 16-move mini-knight tours in blue, red, green and orange.

Step 3:

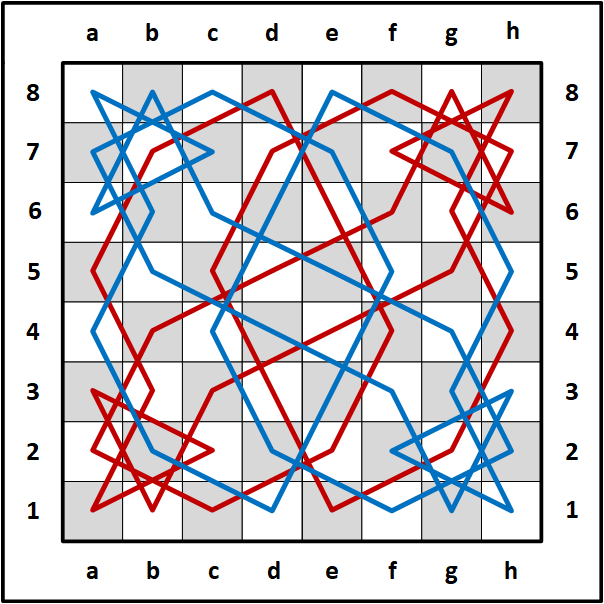
I combined all four mini-knight's tours on one board that ended up making a very nice geometric and symmetrical pattern.  The next image shows the same pattern with two closed 32 knight-move circuits.

Step 4:

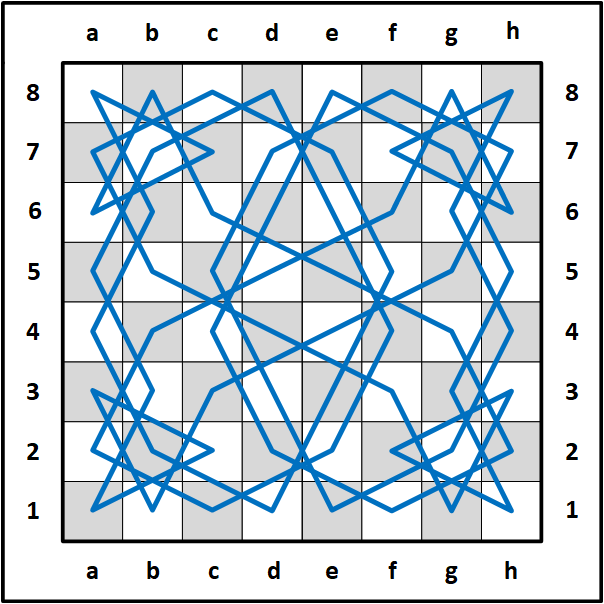
After combining all four mini-knight's tours, I wanted to keep most of the symmetrical pattern but make a single 64 move knight's tour.  I was able to do this by moving only one line (knight move) and deleting one line.  In the following image, I colored all the moves blue.  Next, I added red, orange, and black lines.

Step 5:

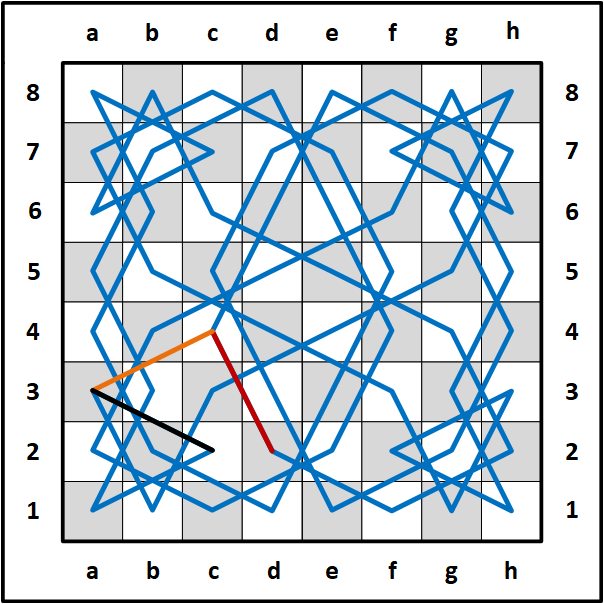
In this step, I moved the red line over the top of the orange line, and deleted the black line then recolored all the lines in the tour back to blue. 

Step 6:

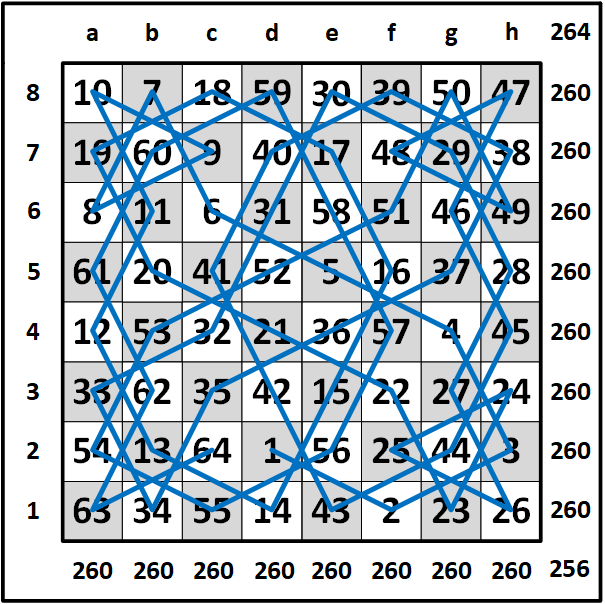
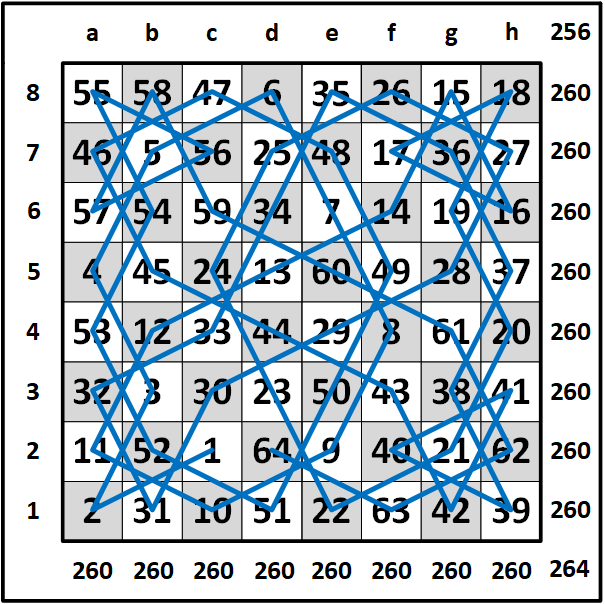
Finally, I renumbered the entire circuit from 1 to 64 starting at d2 with 1 and ending at c2 with 64.  I realized that each row added to 260, each column added to 260, and the diagonals added to 256 and 264 respectively.  Therefore, the following knight's tour is known as a semi-magic knight's tour with all rows and columns adding to 260.  I made another copy of the same moves but started at c2 with 1 and ending at d2 with 64.  The diagonals also added to 256 and 264 respectively.