From Knight Moves to Golden Ratio

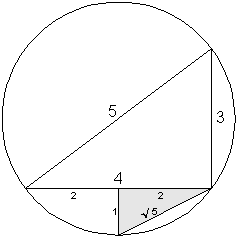
The Knight's move on the chessboard makes an "L" shape pattern. This "L" shape is created by moving the knight two squares horizontally or vertically in any direction, then one square horizontally or vertically. You can also start by moving the Knight one square vertically or horizontally, then two squares vertically or horizontally. The result is a (2:1:sqrt(5)) or (1:2:sqrt(5)) right triangle with the hypotenuse diagonal equaling sqrt (5), which we will call a Knight's-Move Triangle. Adding the hypotenuse (sqrt (5)) to the short side (1), then dividing the result by the long side (2), yields the Golden Ratio (1.618033988749894848204586834365.....), an irrational number known as phi.

The Golden Ratio, or Golden Mean, also known as the Golden Section or Divine Proportion, was used by the Egyptians and the Greeks in some of their great architectural achievements such as the Great Pyramid of Giza and the Parthenon in Athens. Search the Internet for more information about the Golden Ratio, and how it appears in nature, art, and other areas of mathematics. Read The Golden Ratio (the story of phi, the world's most astonishing number) by Mario Livio, Broadway Books, 2002 and The Divine Proportion (a study in mathematical beauty) by H.E. Huntley, Dover Publications, 1970.

The 3:4:5 right triangle can be used to make the Knight's-Move Triangle. Draw a 3:4:5 right triangle where the side lengths are three and four units each, with a hypotenuse of five units. Then draw a circle around the triangle where the circumference of the circle touches all three vertices of the triangle. Next, draw a perpendicular line from the middle of the long side (base) to the perimeter of the circle. Such a construction was discovered by Gabries Bosia. See http://www.math.uwaterloo.ca/~ljdickey/geometry_corner/3-4-5.html.

Concept by Gabries Bosia, Illustrated by Dan Thomasson

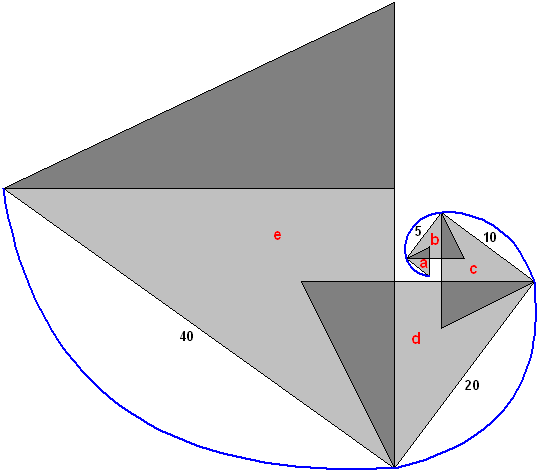
Check out the following spiral I made by continually doubling the size of the hypotenuse of the 3:4:5 right triangle (b - light grey). This spiral is similar to an Archimedean spiral, or more closely related to a Fibonacci spiral, but is constructed by using overlapping isosceles triangles (a, b, c, d, and e). The isosceles triangles are a combination of 3:4:5 right triangles and 1:2:sqrt(5) Knight's-Move Triangles in various proportions. The darker grey triangles are merely Knight's-Move Triangles with the longer side (base) doubling in size. Of course, the same spiral can be created by using only the 3:4:5 right triangles with equally increased proportions.

Select image to view another special spiral. © Dan Thomasson, June 1, 2005

Can Knight's moves on the chessboard make 3:4:5 right triangles? Yes, but not directly. They can be found inside the three basic Knight's Tour polygons (square, rhombus, and diamond). With quarter-inch ruled graph paper, draw a chessboard by using only Knight's moves. Once the chessboard is created, draw the three basic Knight's Tour polygons in the center of the chessboard to make a 2-dimensional cubic shape. After drawing the polygons, find all the 3:4:5 right triangles within the polygons. You will easily notice eight such triangles, but can there be more? Yes, by combining the remaining space not used by the triangles inside the polygons, a 3x4 rectangle can be made. Diagonally divide the rectangle into two halves. Now you have two more 3:4:5 right triangles for a total of ten such triangles from the three Knight's Tour polygons. See the following example:

How many 3:4:5 right triangles can be found in a 17x17 square? The answer is easy. First multiply 17x17 to get 289, then divide 289 by 6 square units per 3:4:5 right triangle to get 48 such triangles with one square unit remaining. Now for the hard part, prove that there are only 48 3:4:5 right triangles in a 17x17 square by drawing them. In the graphic below, there are 40 3:4:5 right triangles that are directly visible.

However, with the remaining space, eight additional 3:4:5 right triangles can be made. There is one single square unit of space left in the middle of the 17x17 square graphic. Thus, 48 total 3:4:5 right triangles exist with one square unit remaining.

Enjoy the following tessellation problems. You can make another problem out of the graphics by showing only the surrounding perimeter of both, and asking if their area is the same, or different.

Speaking of 3:4:5 right triangles, I will share a tessellation I made from Problem 1 shown above. See if you can make a similar tessellation using Problem 2 from above. Experiment with different color combinations, and various sizes of the tessellation piece.