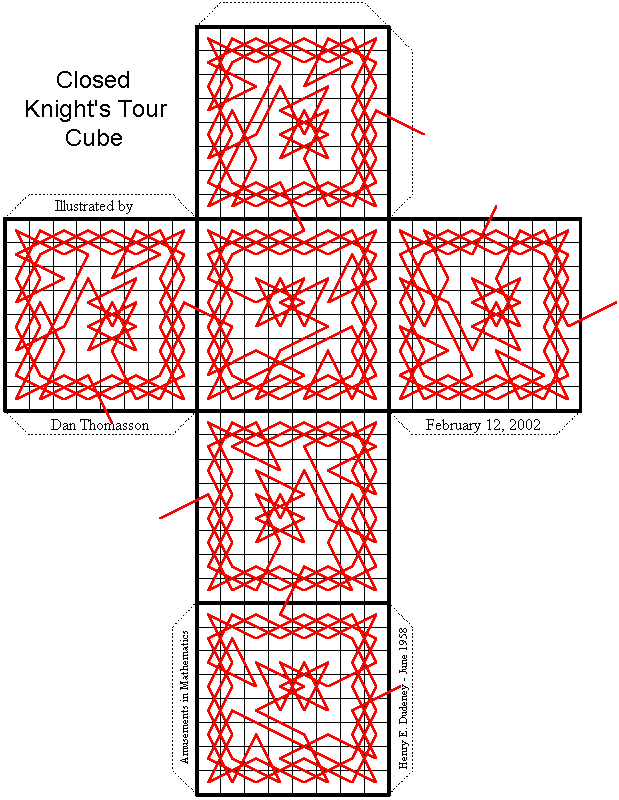
Knight's Tour Cube
The pattern for the Closed Knight's Tour Cube was first seen in the June 1958 book called Amusements in Mathematics, a reproduction of the original 1917 works of Henry Ernest Dudeney. It can also be seen in the 1970 expanded edition on page 229.
Closed Knight's Cube Surface Tour
After re-illustrating the path pattern, I printed a copy of the tour on white 67 lb. cover paper which is light enough to go through almost any printer but strong enough to make into a sturdy cube. I cut around the outside black boarder and dotted lines, then carefully bent each side and tab along the dark black lines. I put a little bit of Elmer's glue on each tab and glued all the sides into a cubic shaped box as shown below.
Knight's Cube Surface Tour by Dan Thomasson
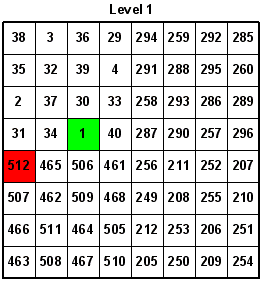
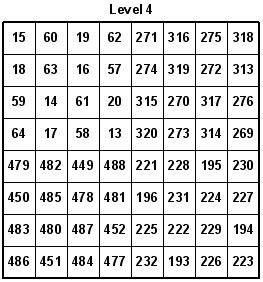
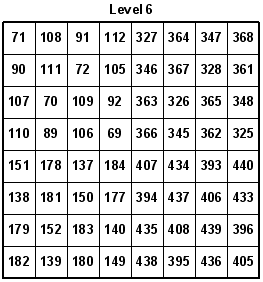
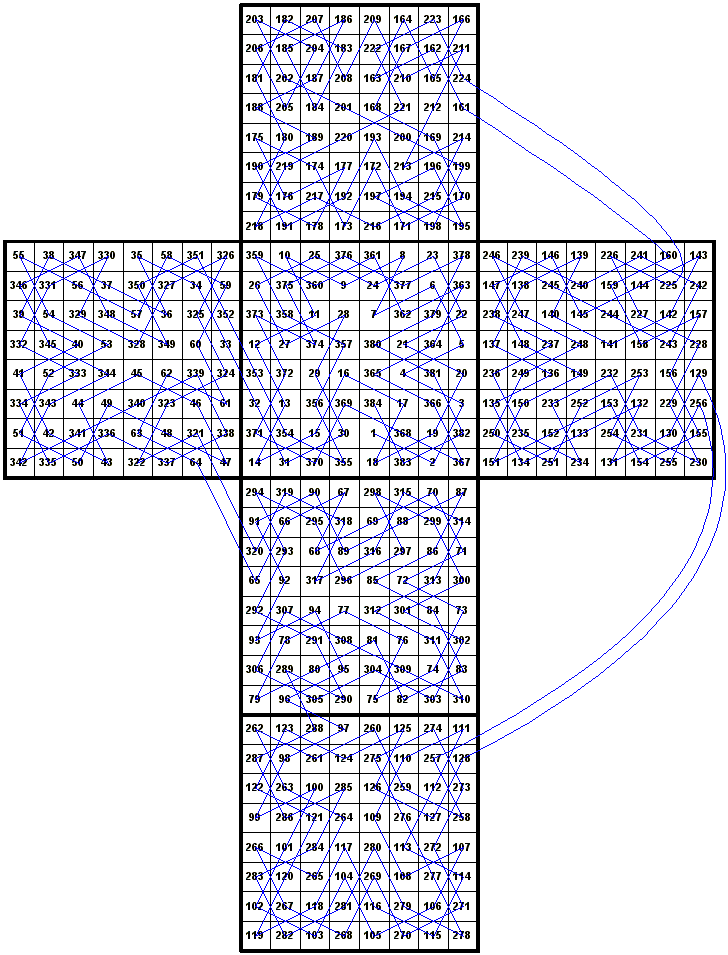
On 11-19-2005, I decided to see if I could make an 8x8x8 Closed Knight's Tour Cube. Without the aid of a computer, it only took me a few minutes to derive at a solution. However, entering 512 numbers on paper to test my theory, and then entering them into the computer to make graphical pictures took much longer. I first made a simple 4x4x4 Knight's Tour Cube, and used its move sequence as a key for solving the 8x8x8 tour. I had to occasionally flip the four 4x4 levels either vertically, or horizontally, to derive at the correct solution for the 8x8x8 tour. This method can be used for easily constructing any size Knight's Tour Cube if it is a multiple of the original 4x4x4 cube size. Look at the following key sequences:
In the process of making the key sequences, I also ended up with the following nice little closed 4x4x4 Knight's Tour Cube that I did not use in the construction of the 8x8x8 tour.
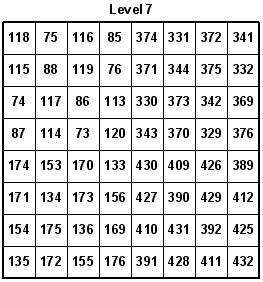
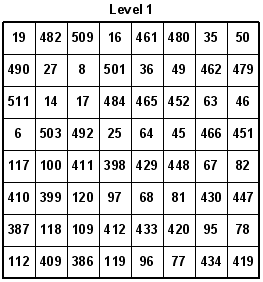
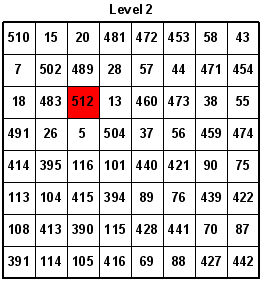
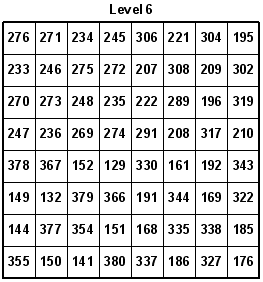
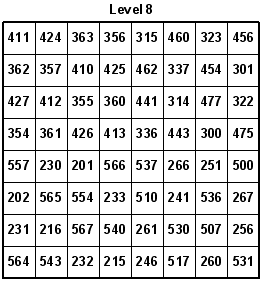
Here are the eight levels of the 8x8x8 Knight's Tour Cube. The accuracy of the numbers was confirmed by Guenter Stertenbrink on 11-20-2005. You may notice that I built the cube in modular sections, using a one-eighth section at a time. Overall, I used eight 4x4x4 cubes in which several have identical Knight's moves.
Knight's Tour Cube-L1
Knight's Tour Cube-L2
Knight's Tour Cube-L3
Knight's Tour Cube-L4
Knight's Tour Cube-L5
Knight's Tour Cube-L6
Knight's Tour Cube-L7
Knight's Tour Cube-L8
Guenter Stertenbrink suggested another possible way of solving 8x8x8 Knight's Tours.
"You could also make a 8*8*8 Closed Knight's Tour by just taking one closed 8*8 tour replicated 8 times. Walk through plane 1, jump to plane 3, walk through the whole plane 3, jump to plane 5, walk through the whole plane 5, jump to plane 7, walk through the whole plane 7, jump to plane 8,... planes 1,3,5,7,8,6,4,2 and back to the start-position."
Guenter's suggestion is very plausible. However, I was only able to make such a tour with the same 8x8 tour replicated seven times with one additional 8x8 tour slightly modified (see Level 2). I made a solution key for solving such 8x8x8 tours. The following graphic shows the 4x4 middle squares of a chessboard. Of course, these same 4x4 squares could also be any matching quadrant of the eight levels (planes) of the 8x8x8 cube (i.e. all top left quadrants). The lower number in each level represents the first move on the 8x8 board, while the higher number represents the very last move on that same board (i.e. on Level 1: 1 = move 1 and 2 = move 64; Level 3: 3 = move 65 and 4 = move 128, …).
"You could also make a 8*8*8 Closed Knight's Tour by just taking one closed 8*8 tour replicated 8 times. Walk through plane 1, jump to plane 3, walk through the whole plane 3, jump to plane 5, walk through the whole plane 5, jump to plane 7, walk through the whole plane 7, jump to plane 8,... planes 1,3,5,7,8,6,4,2 and back to the start-position."
Guenter's suggestion is very plausible. However, I was only able to make such a tour with the same 8x8 tour replicated seven times with one additional 8x8 tour slightly modified (see Level 2). I made a solution key for solving such 8x8x8 tours. The following graphic shows the 4x4 middle squares of a chessboard. Of course, these same 4x4 squares could also be any matching quadrant of the eight levels (planes) of the 8x8x8 cube (i.e. all top left quadrants). The lower number in each level represents the first move on the 8x8 board, while the higher number represents the very last move on that same board (i.e. on Level 1: 1 = move 1 and 2 = move 64; Level 3: 3 = move 65 and 4 = move 128, …).
Knight's Tour Cube Solver
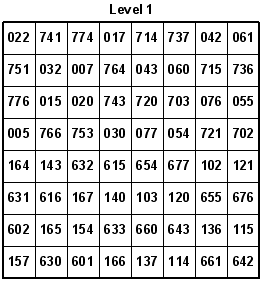
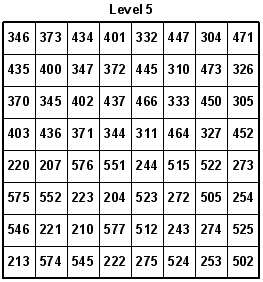
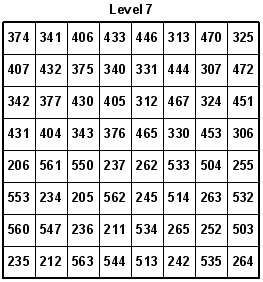
On 04-29-2007, Awani Kumar from India developed the following 8x8x8 Semi-Magic Knight's Tour Cube where all rows, columns, piles, and two of the four main diagonals add up to 2052. The remaining two diagonals add up to 2020 and 2500 respectively.
Kumar's Knight's Tour Cube-L1
Kumar's Knight's Tour Cube-L2
Kumar's Knight's Tour Cube-L3
Kumar's Knight's Tour Cube-L4
Kumar's Knight's Tour Cube-L5
Kumar's Knight's Tour Cube-L6
Kumar's Knight's Tour Cube-L7
Kumar's Knight's Tour Cube-L8
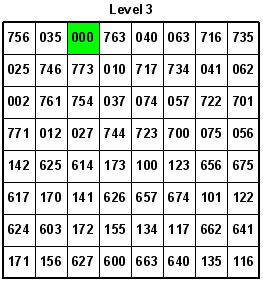
On 04-30-2007, Guenter Stertenbrink converted Awani Kumar's Semi-Magic Knight's Tour Cube into octal numbers ranging from 000 to 777 (511 decimal). Using gematria, the number 777 has several divine attributes. 777 is also the total number of pages in the Pulitzer prize-winner 20th-anniversary edition of Gödel, Escher, Bach: An Eternal Golden Braid by Douglas R. Hofstadter.
Each row, column, or pile adds up to 3774 (octal). Convert 3774 octal back to decimal to get 2044. Remember that each number is one less per move because of starting the tour at zero instead of one. Therefore, just add 2044 plus 8 to get the original 2052 total for each row, column, or pile in Awani Kumar's Knight's Tour Cube.
Interestingly, a total of 34 octal (28 decimal) can be obtained by adding up only the leftmost digits, only the middle digits, or only the rightmost digits of the three-digit octal numbers per row, column, or pile.
Each row, column, or pile adds up to 3774 (octal). Convert 3774 octal back to decimal to get 2044. Remember that each number is one less per move because of starting the tour at zero instead of one. Therefore, just add 2044 plus 8 to get the original 2052 total for each row, column, or pile in Awani Kumar's Knight's Tour Cube.
Interestingly, a total of 34 octal (28 decimal) can be obtained by adding up only the leftmost digits, only the middle digits, or only the rightmost digits of the three-digit octal numbers per row, column, or pile.
Octal Knight's Tour Cube-L1
Octal Knight's Tour Cube-L2
Octal Knight's Tour Cube-L3
Octal Knight's Tour Cube-L4
Octal Knight's Tour Cube-L5
Octal Knight's Tour Cube-L6
Octal Knight's Tour Cube-L7
Octal Knight's Tour Cube-L8
Also, Awani made a Knight's Tour on the surface of a cube similar to Dudeney's, yet it is semi-magic where all rows and columns add up to 1540 on each face of the cube.
© Awani Kumar - May 3, 2007
Illustrated by Dan Thomasson