Solving Knight's Tours with Number Pairs
Number Pairs 49-81 by Dan Thomasson July 14, 2001
Several people have requested that I share my basic mathematics for solving Knight's Tours with number pairs. Here is my process. I know there are 64 squares on a regular chessboard. If each square is assigned a number from 1-64 covering all 64 numbers, they would add up to 2080 total. I want each quadrant to add up to 520. I also want each row and column in each quadrant to add up to 130. I know that if I take (1+64) + (2+63) they add up to 130.
If I repeat the pattern, I will end up with a method for putting four numbers together that all add up to 130 for each row in a quadrant. However, this method does not yield a complete Knight's Tour sequence because of the 32/33 number pair.
In order to create the number pairs to make complete Knight's Tour moves, I use the same method but modify it just a little. I will show you both. I connect columns A + D together and columns B + C together to make new number pairs shown on the right side of the Number Pair Process image below.
If I repeat the pattern, I will end up with a method for putting four numbers together that all add up to 130 for each row in a quadrant. However, this method does not yield a complete Knight's Tour sequence because of the 32/33 number pair.
In order to create the number pairs to make complete Knight's Tour moves, I use the same method but modify it just a little. I will show you both. I connect columns A + D together and columns B + C together to make new number pairs shown on the right side of the Number Pair Process image below.
Number Pair Process by Dan Thomasson, July 14, 2001
Now I am able to use the number pairs shown on the right side of the chart above to create Open Knight's Tours. When you look at the following page, you will see a couple ways I used the numbers to create Solution-1 and Solution-2.
The Board-1 - Puzzle Pieces and Board-2 - Puzzle Pieces below can be used to easily create Knight's Tours. All you have to do is print both boards and cut around the dotted lines. You should end up with 64 vertical pairs of numbers.
The Board-1 - Puzzle Pieces and Board-2 - Puzzle Pieces below can be used to easily create Knight's Tours. All you have to do is print both boards and cut around the dotted lines. You should end up with 64 vertical pairs of numbers.
Board-1 - Knight's Tour Puzzle pieces. by Dan Thomasson, July 14, 2001
Board-2 - Knight's Tour Puzzle pieces. by Dan Thomasson, July 14, 2001
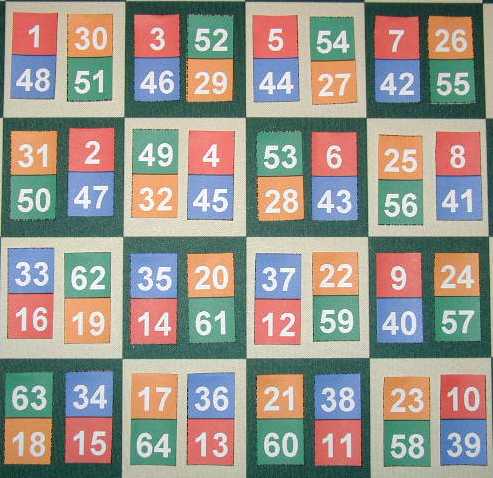
I lay out the numbers cut from Board-1 in numerical order across the first two rows of squares on a standard tournament chess board. Two pairs of numbers fits nicely in one square each. I then lay out the numbers cut from Board-2 in numerical order across the bottom two rows of squares on the board.
Take a look at Solution-1 and Solution-2 below. You will notice how I arranged the numbers 1-16 in an alternating pattern around the boards. What appears to work best is having 1-4, 5-8, 9-12, and 13-16 in their own quadrant respectively, though there may be other solutions. Pay close attention to the number pairs 1/48, 32/49, 16/33, and 17/64. They are the key to successfully making many different Knight's Tours.
Solution-1
Now I am able to use the 4x4 squares in the center of the standard chess board to begin designing my Knight's Tour. I like to put the four key pairs of numbers listed above (1/48, 32/49, 16/33, and 17/64) on the board first so that they connect correctly in a Knight's move sequence.
I then continue with 2-15 in an alternating pattern around the board. After covering every other vertical pair of squares with the red/blue colors, I look at the 32/49 pair and start placing 50-63 on the board where 63's last move will connect to number 64 with a Knight's move.
Solution-1 using Number Pairs 49-81 - by Dan Thomasson, July 14, 2001
The images above show how I created Solution-1. The series of four images below show how I created Solution-2.
Solution-2
Solution-2 using Number Pairs 49-81 - by Dan Thomasson, July 14, 2001
Need some tips on starting the tours? Select KT SMKT-Tips.
After successfully creating a tour, I copy the moves on a simple chessboard in Microsoft Excel. I then recreate that board in Visio to connect the numerical sequence with red lines. This same process can be done in any paint type program or just manually drawn on paper.
Still having problems solving your own Knight's Tours using these number pairs? Select Solutions.
Several years have now passed since creating my first tours using number pairs in 2001. The solutions I've provided can be confirmed at 140 Semi-Magic Knight's Tours. Keep in mind that when rotating, reflecting, or reversing a tour, 16 Separate Knight's Tours can be obtained from the original tour. Therefore, it is possible to have 240 separate tours from the original 15 unique tour solutions.
After successfully creating a tour, I copy the moves on a simple chessboard in Microsoft Excel. I then recreate that board in Visio to connect the numerical sequence with red lines. This same process can be done in any paint type program or just manually drawn on paper.
Still having problems solving your own Knight's Tours using these number pairs? Select Solutions.
Several years have now passed since creating my first tours using number pairs in 2001. The solutions I've provided can be confirmed at 140 Semi-Magic Knight's Tours. Keep in mind that when rotating, reflecting, or reversing a tour, 16 Separate Knight's Tours can be obtained from the original tour. Therefore, it is possible to have 240 separate tours from the original 15 unique tour solutions.