Thomasson Cube
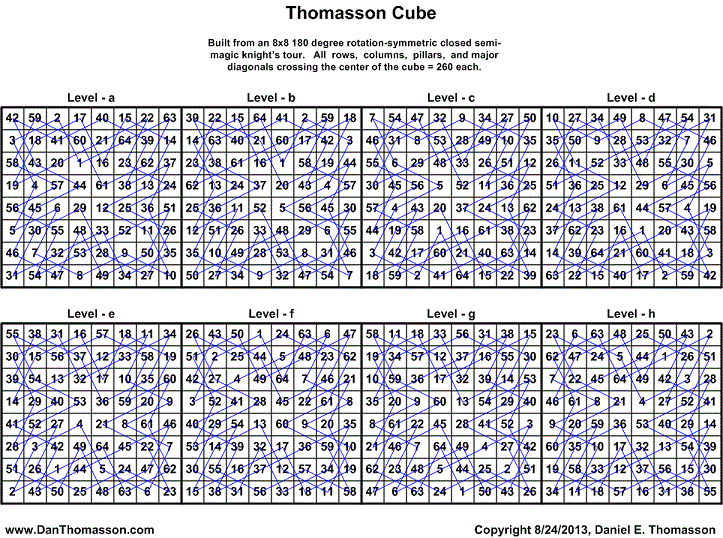
I designed the 4x4x4 closed knight's tour in the banner above back in 2005. I constructed the following 8x8x8 180 degree rotation-symmetric Thomasson Cube from a single closed knight's tour that is also 180 degree rotation symmetric. All the rows, columns, pillars, and 4 triagonals (diagonals crossing the center of the cube) add up to 260 each. Re-arranging the levels out of 8! or 40,320 permutations yield 904 cube solutions with the same properties. Of the 904 solutions, 452 are reflections. Reflections mean that when reversing the order of the levels, a mirror image of the cube is created (abcdefgh makes hgfedcba). Thus, there are 452 unique solutions that when reversed yields an additional 452 solutions. See Thomasson Cube Solutions for a list of all solutions.
Thomasson Cube-2
The following 8x8x8 cube is similar to the Thomasson Cube shown above except that I constructed it from a half-symmetric closed semi-magic knight's tour. See Thomasson Cube-2 Solutions for all possible solutions of re-arranging the levels of the cube and still having all rows, columns, pillars, and triagonals equal 260 each. There are 372 solutions with 186 reflections.
Thomasson Cube-3
The following 8x8x8 cube is very similar to Thomasson Cube-2. I also constructed it from a half-symmetric closed semi-magic knight's tour. Notice that both the path pattern and number sequences in the top half of each level is identical to Thomasson Cube-2 with just the levels from Level-e to Level-h re-arranged in Thomasson Cube-3. See Thomasson Cube-3 Solutions for all possible solutions of re-arranging the levels of the cube and still having all rows, columns, pillars, and triagonals equal 260 each. There are 248 solutions with 124 reflections.
Thomasson Cube-4a
The following 8x8x8 cube is constructed from a half-symmetric closed semi-magic knight's tour. This knight's tour path pattern is unique in that it makes five special cubes with different number sequences Of the five cubes, there are a total of 4,096 solutions out of 5*8! or 201,600 permutations. See Thomasson Cube-4a Solutions for all possible solutions of re-arranging the levels of the cube and still having all rows, columns, pillars, and triagonals equal 260 each. There are 1280 solutions with 640 reflections.
Thomasson Cube-4b
The following 8x8x8 cube is constructed from the same half-symmetric closed semi-magic knight's tour as in Thomasson Cube-4a. See Thomasson Cube-4b Solutions for all possible solutions of re-arranging the levels of the cube and still having all rows, columns, pillars, and triagonals equal 260 each. Notice that only Level-f and Level-g have changed from Thomasson Cube-4a. There are 880 solutions with 440 reflections.
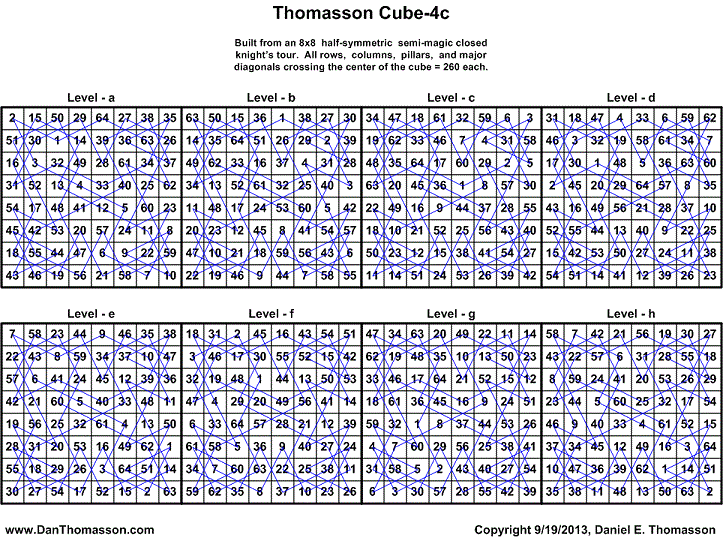
Thomasson Cube-4c
The following 8x8x8 cube is constructed from the same half-symmetric closed semi-magic knight's tour as in Cube-4b and Cube-4a. See Thomasson Cube-4c Solutions for all possible solutions of re-arranging the levels of the cube and still having all rows, columns, pillars, and triagonals equal 260 each. There are also 880 solutions with 440 reflections as in Thomasson Cube-4b.
Thomasson Cube-4d
The following 8x8x8 cube is constructed from the same half-symmetric closed semi-magic knight's tour as in Cube-4a, Cube-4b, and Cube-4c See Thomasson Cube-4d Solutions for all possible solutions of re-arranging the levels of the cube and still having all rows, columns, pillars, and triagonals equal 260 each. There are 528 solutions with 264 reflections.
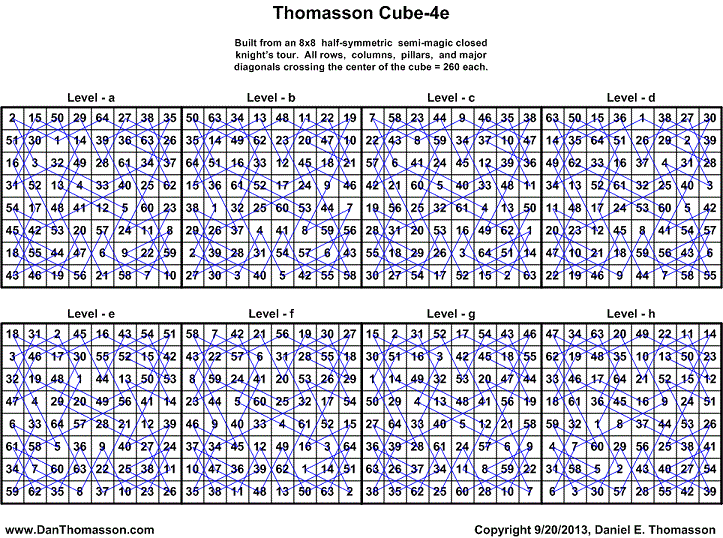
Thomasson Cube-4e
The following 8x8x8 cube is constructed from the same half-symmetric closed semi-magic knight's tour as in Cube-4a, Cube-4b, Cube-4c, and Cube-4d. See Thomasson Cube-4e Solutions for all possible solutions of re-arranging the levels of the cube and still having all rows, columns, pillars, and triagonals equal 260 each. There are also 528 solutions with 264 reflections as in Thomasson Cube-4d.
Thomasson Cube-5
On 9/20/2013, I developed Thomasson Cube-5 (a 128 x 128 x 128 cube) by combining all 4096 8x8x8 cube solutions from Thomasson Cubes 4a, 4b, 4c, 4d, and 4e. All rows, columns, pillars, and triagonals equal 4160 each. There are 128! times 4096! for a total of 1.404 e+13235 different solutions.
Thomasson Cube-6 to Cube-82
Though not as visually pleasing as the closed knight tours shown above, on 10/10/2013 I found that all 77 (Thomasson Cube-6 to Cube-82) opened semi-magic knight tours make cubes where all rows, columns, pillars, and triagonals (also known as space diagonals or the 4 main diagonals crossing the center of the cube) equal 260 each by adding reversals of the path and rotations of the tour. In Thomasson Cube-6, there are 384 solutions with 192 reflections. See Thomasson Cube-6 Solutions. A mirror image of this cube and all other 77 opened semi-magic knight tours can also be constructed providing similar results. For this webpage, I will only show the first opened tour example.
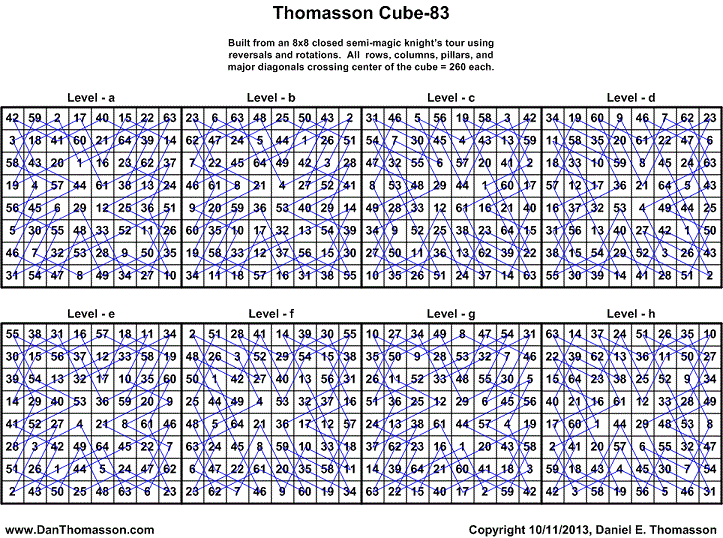
Thomasson Cube-83 to Cube 145
On 10/11/2013 I also discovered that all 63 (Thomasson Cube-83 to Cube-145) closed semi-magic knight tours make cubes where all rows, columns, pillars, and triagonals equal 260 each by adding reversals of the path and rotations of the tour as in Thomasson Cube-6 shown above. I constructed Thomasson Cube-83 by using only level-a and level-h of my original Thomasson Cube shown at the top of this webpage. See Thomasson Cube-83 Solutions containing 896 solutions with 448 reflections.
Thomasson Cube Solutions
If you would like to see solutions for any of the other opened or closed semi-magic knight tours not shown on this webpage, please contact me by selecting the email icon next to Social Media at the top-right corner of this page. Use the following SMKT graphic file to select the tour or tours you are requesting. There are 14 rows with 10 semi-magic tours in each row. The top row is '1' and the bottom row is '14.' Each column should be labeled 'a' through 'j.' Therefore, 1a is the top-left semi-magic knight's tour. For further information about the origination of the following graphic and how all semi-magic knight tours were found, see MagicTour.free.fr.
Thomasson's Magic Cube Method
To find all solutions for each of the above Thomasson Cubes, I wrote a program using Microsoft Small Basic. This program checks all permutations of rearranged levels of the cube to find the solutions. If the cube size is 8x8x8, there would be 8! or 40320 permutations (different ways of arranging the levels). This method can be used for any magic cube to find all possible solutions of rearranging the levels of the cube thus making new magic cubes. Download the following Excel file to see the solutions for a Perfect (Nasik) 8x8x8 Magic Cube that my program found.